Elbow Method vs Silhouette Method: Which is Better for Finding Optimal K?
By Mbali Kalirane on

The Elbow and Silhouette Methods are popular methods used for finding the value of \(K\) in K-means clustering. In this article we’ll look at the difference between the Silhouette and Elbow Methods when applied to k-means clustering. To get a better understanding of these methods, we’ll first take a look at how k-means clustering works.
Table of Contents
- What’s K-Means Clustering
- How Does K-Means Ensure Accurate Clustering of Elements?
- What is Elbow Method for finding K?
- What’s the Silhouette Method for finding K?
- Conclusion
- Sources
What’s K-Means Clustering?
K-Means clustering partitions a dataset into different clusters according to the proximity of its data points to each other. In the real world, this ‘proximity’ between the data point could be expressed as the ‘similarity’ between the data points. For example, K-Means could segment customers according to similarity of age, gender or purchase behavior. But mathematically, this similarity is expressed numerically as ‘proximity’ to make it possible to measure. This proximity is typically measured using the Euclidean distance, and is used for determining which data points are closest enough to each other to be placed into a common cluster. This pretty much sums up the whole aim of K-Means clustering.
K-Means clustering aims to ensure that elements in a single cluster have more similarity to each other than to elements of other clusters. In other words, elements within a single cluster must be closer to each other than to elements of other clusters.
To achieve this minimum proximity, the K-Means algorithm focuses on minimizing the distance between every data point and its centroid. It does this by minimizing the cost function, the Within Cluster Sum of Squares (WCSS), which represents the variation within each cluster. The aim is to minimize the WCSS as much as possible such that there is an adequate number of data points within each cluster. The WCSS is the sum of Euclidean distances from the data points to their centroids, given by:
\[WCSS = \sum_{i=1}^{k} \sum_{x \in C_i} ||x - \mu_i||^2\]| where, | x - \mu_i | is the Euclidean distance between a point and a centroid. |
The purpose of the cost function is that it helps evaluate the performance of the clustering. Minimizing the cost function ensures that the data points which are closest to each other stay in the same cluster and that the clustering works as intended.
How Does K-Means Ensure Accurate Clustering of Elements?
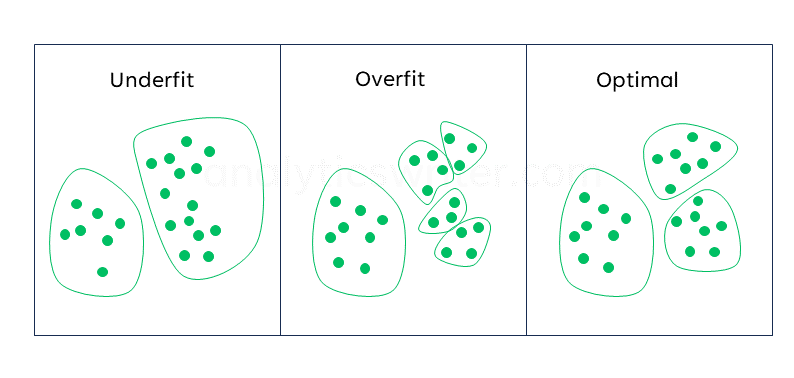
The number of clusters is typically a pre-selected parameter in K-means. For the K-Means algorithm to achieve its aim of putting similar elements in a single cluster, the number of clusters chosen need to be adequate. When the number of clusters chosen is too low, a problem can arise where elements of distant proximity are put in one cluster (underfitting). And when the number of clusters chosen is too high, elements which are similar to each other could be separated from each other (overfitting). Choosing the wrong \(K\) obviously defeats the purpose of K-Means, which is to ensure that similar objects are clustered together.
So, to ensure that distant elements aren’t put in the same cluster or that similar elements aren’t separated from each other, we need to ensure that we find the correct value of \(k\). Fortunately, there are several methods that can help find the optimal value of \(k\). In this article, I will be focusing on the Elbow and Silhouette Methods.
What is Elbow Method for finding K?
The elbow method is a method for finding the optimal value of K. When applying K-means to data, the change in the variation with clusters or the WCSS decreases rapidly. This is because increasing the number of clusters tends to reduce the distance between data points and their respective centroids, thereby decreasing the within-cluster variation. There then becomes a certain point where increasing the number of clusters \(k\) leads to change in WCSS slowing down. This is called the elbow point and the Elbow method is used to find this point.
As the value of \(K\) increases, the variability between the points decreases, because we end up with similar points in a cluster, and so the WCSS becomes smaller. This happens because, as the number of clusters increase, the size of the clusters becomes smaller as they have less elements. As a result, a small cluster with a small number of elements is likely to have a small variation between data points. In extreme cases, a single cluster could contain only one element.
Having one element per cluster will result in a WCSS of zero, and that is not what we want. Although K-Means aims to minimize the WCSS, it aims to minimize WCSS as much as possible, while still having a high enough number of data points in a cluster. We aim to have a low WCSS but that’s not zero.
The steps of the Elbow method are as follows:
- Calculate clustering algorithm with different values of \(k\)
- Calculate the total WCSS for all the values of \(k\)
- Plot the WCSS with respect to the number of clusters.
- Find the point at which the plot forms an elbow. This point is the optimal \(k\).
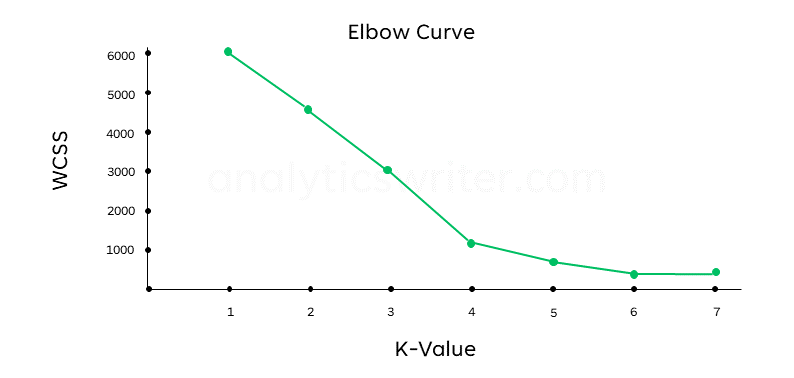
As stated previously, the WCSS decreases as the value of \(k\) increases. This rate of decrease changes at the point of the elbow. The WCSS decreases quickly for small values of \(k\) and eventually, as \(k\) becomes larger, the decreasing slows leading to the formation of an elbow point, where there’s a change of speed. The point where this change of speed occurs is called the optimal value of K. In the below elbow curve, this elbow point occurs at k=4:
What’s the Silhouette Method for finding K?
As said before, the aim of clustering is to ensure that objects within one cluster are more similar to each other than objects in other clusters. The similarity of objects within one group is called cohesion, and the difference of the objects from other clusters is called separation.
We use the Silhouette coefficient to measure the cohesion and separation together to find out how well our clusters are formed. Cohesion is calculated by a variable, \(a\), which is the average of the distances within a cluster from a specific chosen value in the cluster. Separation is calculated by a variable \(b\), which is the average of the distances from the chosen point in the cluster to all the points in the nearest cluster.
Silhouette measures how similar a data point is within a cluster compared to other clusters. The silhouette method consists of calculating silhouette coefficients at each point to compare the similarity of that point compared to other clusters. The silhouette coefficient ranges from -1 to 1. A low value indicates that a point is well-matched with points within its own cluster but far off from points in other clusters.
Because a measures cohesion and b measures separation, b should be as large as possible and a as small as possible. This is because the aim of the Silhouette method is to aim for the Silhouette coefficient to as close to 1 as possible.
If many of the points are close to 1, then it’s most likely that the number of clusters is correct. However, if the points are close to -1, then it’s highly likely that the number of clusters chosen is too high or too low.
The steps of calculating the Silhouette Coefficient are as Follows:
- Calculate $b$ the distance between a particular point in a cluster and all of the other points in that cluster.
- Calculate \(a\) the distance between that point and all the points in the cluster nearest to its own cluster.
-
Calculate \(S\) the Silhouette coefficient by using the formula below:
\[S=(b-a )/(max(a,b))\]
This is the Silhouette coefficient for the chosen data point. To normalize the Silhouette coefficient, we divide $b-a$ by $max(a,b)$. We want to measure it on the same scale. We then plot the Silhouettes for each cluster to find the points that are outliers. Choose the number of clusters with the least amount of outliers and larger positive values.
Below is an example of a silhouette analysis, showing the silhouette coefficients for each class. Class 2 is shown to be the most optimal, having a silhouette coefficient of about 0.9.
Conclusion
The Silhouette and Elbow methods are a type of hyperparameter tuning, where \(K\) is the hyperparameter that is tuned to find its optimal value. The elbow method is suitable when clusters are well-separated and distinct, leading to a noticeable “elbow” point on the plot. However, it may not perform well when clusters are overlapping or irregularly shaped. The silhouette method, on the other hand, is better able to perform with irregularly shaped clusters and overlapping data points. It provides a quantitative measure of cluster quality, making it useful for a wide range of datasets. In practice, it’s beneficial to use both methods in together and compare their results to make a more informed decision about the optimal number of clusters.
Key Take Aways
- The aim of k-means clustering is to ensure that points in a certain cluster are more similar to each other than points in other clusters. This is separation and cohesion. It calculates the distance between points using the WCSS.
- Elbow method works by finding the elbow point, which is the point where increasing $k$, slows down the change in WCSS. This is the optimal point.
- Silhouette method works on the principle of cohesion and separation to calculate the silhouette coefficient. Cohesion is represented by \(a\) and separation by \(b\). \(b\) should be large and \(a\) should be small. The Silhouette coefficient measures how good the number of clusters are.